Vector의 내적과 외적
2018-07-29 | 알고리즘 CCW Vector벡터의 내적 (Inner product)
- scalar product 혹은 dot product라고도 함
- 두 벡터의 내적의 결과는 스칼라 값
- 𝐴 ⃗ = <𝑨𝒙, A𝒚>, 𝐵 ⃗ = <B𝒙, 𝑩𝒚>라 할 때
𝐴 ⃗∙𝐵 ⃗ = 𝑨𝒙 × 𝑩𝒙 + 𝑨𝒚 × 𝑩𝒚 = |𝐵 ⃗| × |𝐴 ⃗|cos𝜃 = |𝐴 ⃗||𝐵 ⃗|cos𝜃
1. 벡터의 내적을 통해 상대적인 방향을 구할 수 있다
𝐴 ⃗∙𝐵 ⃗ = |𝐴 ⃗||𝐵 ⃗|cos𝜃
내적의 결과를 통해 𝜃을 알 수 있다.
- 양수인 경우 ->
𝜃 < 90도 - 음수인 경우 ->
𝜃 > 90도 - 0인 경우 ->
𝜃 = 90도
벡터의 외적(Cross product)
- 외적의 결과는 또 다른 벡터의 값
- 𝐴 ⃗ = <𝑨𝒙, 𝑨𝒚, 𝑨𝒛>, 𝐵 ⃗ = <𝑩𝒙, 𝑩𝒚, 𝑩𝒛>일 때

1. 벡터의 외적을 통해 CCW, CW 판단

두 벡터의 외적(𝐴 ⃗×𝐵 ⃗)을 구하면
오른손 법칙을 이용하여 두 벡터의 방향을 구할 수 있다. 반시계방향(CCW)이거나 시계방향(CW)인지를 알 수 있다.
2차원에서는 z = 0이므로 위 외적 공식에서 z = 0을 대입하면 아래와 같이 나온다.
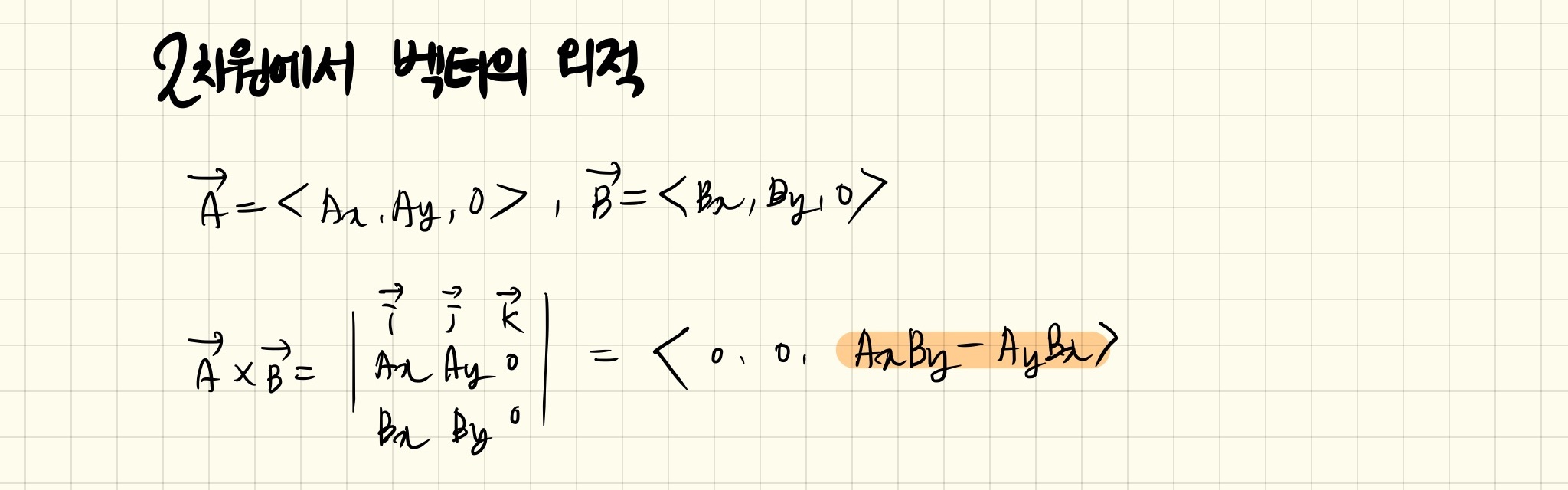
=> 오른속 법칙을 이용하여 AxBy - AyBx값을 가지고 두 벡터가 시계 방향인지 반시계 방향인지 알 수 있다.
- i)
AxBy - AyBx> 0 -> CCW - ii)
AxBy - AyBx< 0 -> CW
2. 벡터의 외적을 통해 두 선분의 교차여부를 판단
기본 아이디어
두 선분 AB, CD가 있고 두 선분이 교차한다면, 점 A를 기준으로 CD의 각 끝점 C, D는 각각 반시계방향과 시계방향일 것이다.
- i) ABC가 반시계방향이고 ABD가 시계방향
- ii) ABC가 시계방향이고 ABD가 반시계방향
3. 벡터의 외적을 통해 삼각형 넓이 구하기
평행사변형의 넓이
S = |𝐴 ⃗ x 𝐵 ⃗|
삼각형의 넓이
S = 𝟏/𝟐 × |𝐴 ⃗x𝐵 ⃗|
Q. 다각형의 넓이는 어떻게 구할까?
여러개의 점 중 하나의 점을 꼭지점으로 하는 삼각형들로 구성된 다각형이라고 생각한다면 쉽다. 삼각형의 넓이를 구하는 공식을 이용하여 풀면 된다.
- 좋은 참고 글 : 다크 프로그래머 - 다각형 도형의 면적(넓이) 구하기

